751.10 General Superstructure: Difference between revisions
m attached article to new EPG 751 |
m →751.10.1.6 Slab Overhang Section Design: minor clarification |
||
| Line 731: | Line 731: | ||
'''Determining Top Reinforcing''' | '''Determining Top Reinforcing''' | ||
The top (negative) reinforcing steel may be determined by assuming the section to be either singly- or doubly-reinforced, as needed. For slab overhang lengths equal to or less than 3’-10”, the reinforcement shown in the standard slab details is adequate (see | The top (negative) reinforcing steel may be determined by assuming the section to be either singly- or doubly-reinforced, as needed. For slab overhang lengths equal to or less than 3’-10”, the reinforcement shown in the standard slab details is adequate (see EPG 751.10.1.7). For overhang lengths greater than 3’-10”, further analysis is required for top transverse steel design. | ||
Revision as of 07:24, 27 April 2010
751.10.1 Slab on Girder
751.10.1.1 Material Properties
| Concrete | ||
|---|---|---|
| Unit weight of reinforced concrete, | = 150 | |
| Concrete Slab on Girders shall consist of: | ||
| Class B-2 Concrete | = 4.0 ksi | |
| = 8 | ||
| Concrete modulus of elasticity, | = 33000 | |
| Where: | ||
| = Unit weight of non-reinforced concrete = 0.145 kcf | ||
| Modulus of rupture: | ||
| For minimum reinforcement, | = 0.37 | |
| For deflection, camber and | ||
| distribution reinforcement | = 0.24 | |
| Safety Barrier Curbs | ||
| Safety Barrier Curbs shall consist of: | ||
| Class B-1 Concrete | = 4.0 ksi | |
| = 8 | ||
| Median Barrier Curbs | ||
| Median Barrier Curbs shall consist of: | ||
| Class B-1 Concrete | = 4.0 ksi | |
| = 8 | ||
| Future Wearing Surface | ||
| Unit weight of future wearing surface, | = 140 | |
| Reinforcing steel | ||
| Minimum yield strength, | = 60.0 ksi | |
| Steel modulus of elasticity | = 29000 ksi | |
751.10.1.2 Limit States and Load Factors
In general, each component shall satisfy the following equation:
Where:
| = Total factored force effect | |
| = Force effect | |
| = Load modifier | |
| = Load factor | |
| = Resistance factor | |
| = Nominal resistance | |
| = Factored resistance |
Limit States
The following limit states shall be considered for slab interior and overhang design:
| For slab interior design: | STRENGTH – I<br\>SERVICE – I* |
| For slab overhang design: | EXTREME EVENT – II<br\>STRENGTH – I<br\>SERVICE – I* |
| *Of deformation, cracking, and concrete stresses, only cracking<br\>need be considered here. | |
| FATIGUE limit state need not be investigated for concrete decks<br\>in multi-girder bridges due to observed performance and laboratory<br\>testing. | |
Resistance factors
For STRENGTH limit state,
- Flexure and tension of reinforced concrete, = 0.90
- Shear and torsion, = 0.90
For all other limit states, = 1.00
751.10.1.3 Loads
Permanent (Dead) Loads
Permanent loads include the following:
- Slab weight
- Future Wearing Surface
- A 3” thick future wearing surface (35psf) shall be considered on the roadway.
- Safety Barrier Curb (SBC)
- For slab overhang design, assume the weight of the SBC acts at the centroid of the SBC.

(*) 12" for slab design (LRFD (3.6.1.3.1), 2'-0" for other design
Application of Live Load to Slab
Gravity Live Loads<br\>
Gravity live loads include vehicular, dynamic load allowance, and pedestrian loads.
- Vehicular
- The design vehicular live load HL-93 shall be used. It consists of either the design truck or a combination of design truck and design lane load.
- For slab design, where the equivalent strip method is used, the force effects shall be determined on the following basis:
- Where primary strips are transverse the design shall be based on the truck alone.
- Where primary strips are transverse and their span exceeds 15 ft – the design shall be based on the truck and lane load. For the purpose of slab design, the lane load consists of a load equal to 64 psf uniformly distributed over 10 feet in the transverse direction.
Dynamic Load Allowance<br\>
The dynamic load allowance replaces the effect of impact used in AASHTO Standard Specifications. It accounts for wheel load impact from moving vehicles. For slabs, the static effect of the vehicle live load shall be increased by the percentage specified in Table below.
| Slab Component | IM |
|---|---|
| Deck Joints – All Limit States | 75% |
| All Other Limit States | 33% |
The factor to be applied to the static load shall be taken as:
The dynamic load allowance is not to be applied to pedestrian or design lane loads.
Multiple Presence Factor, m:
The multiple presence factor accounts for the probability for multiple trucks passing over a multilane bridge simultaneously.
| m = | 1.20 for 1 Loaded Lane |
| 1.00 for 2 Loaded Lanes | |
| 0.85 for 3 Loaded Lanes | |
| 0.65 for more than 3 Loaded Lanes |
Pedestrian
Pedestrian live load on sidewalks greater than 2 ft wide shall be:
| PL = | 0.075 ksf |
This does not include bridges designed exclusively for pedestrians or bicycles.
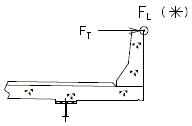
Collision Loads
Collision loads applied to the safety barrier curb (SBC) shall be transferred to the slab overhang. The design forces from SBC consist of lateral and vertical components that are to be considered separately. Because of MoDOT’s experience with the collision survivability of bridge decks that utilize the standard barriers, MoDOT does not require the deck overhang to be designed for forces in excess of those resulting from the design loads for Traffic Railings shown in LRFD Table A13.2-1. The standard slab crosssections reflect this design philosophy.
- Design Case 1
- The collision force and moment shall be considered.
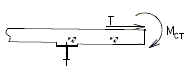
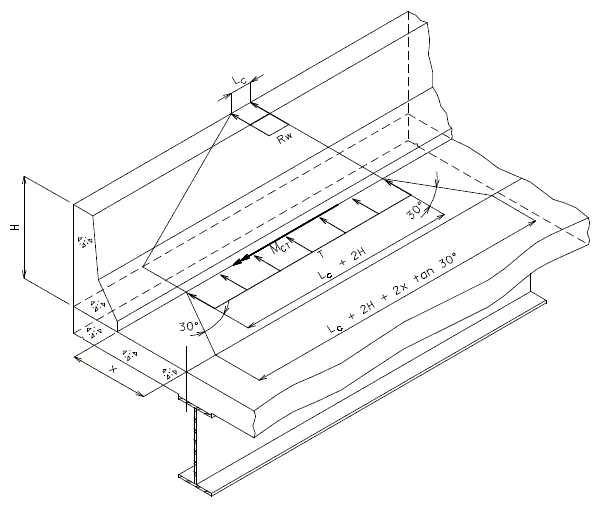
- Slab Overhang Design Collision Moment
- The design collision moment at the base of the curb is the barrier curb moment capacity about the curb longitudinal axis. For SBC design with either failure mechanism 1 or 2 controlling:
- (averaged over height of SBC)
- Slab Overhang Design Collision Force
- A refined analysis may be preformed. In this case the design collision moment at the base of the curb, Mct, is to be taken as the average moment over the theoretical distribution length (Lc+2H for continuous sections), when the TL-4 collision load is applied to the top of the curb.
- For continuous sections of safety barrier curbs:
- Where:
= total transverse resistance of curb (k) = critical length of yield line failure pattern (ft) = height of curb (ft) = tensile force per unit of deck length at base of curb (k/ft)
- For discontinuous safety barrier curb sections:

Transfer of Safety Barrier Curb Collision Forces
Transfer of Safety Barrier Curb Collision Forces751.10.1.4 Design and Analysis Methods
Equivalent Strip Method
The equivalent strip method is an approximate method of analysis in which the reinforcing steel is designed using a certain width of deck to resist the applied loading. Where the strip method is used, the extreme positive moment in any slab section between girders shall be taken to apply to all positive moment regions, and similarly with extreme negative moments.
There are other methods of analysis allowed, such as finite element method, but the equivalent strip method is recommended.
751.10.1.5 Interior Section Design
Slab Thickness
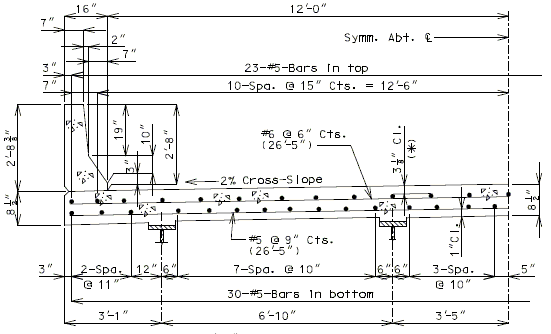
The slab portion between girders shall be 8 1/2” thick for both the C.I.P. and precast panel options. Precast panel option is preferred when allowed.
Design Cases
Two design cases shall be considered for each design condition.
Design Case 1 STRENGTH I load combination for reinforcing design.
Design Case 2 SERVICE I load combination for cracking check.
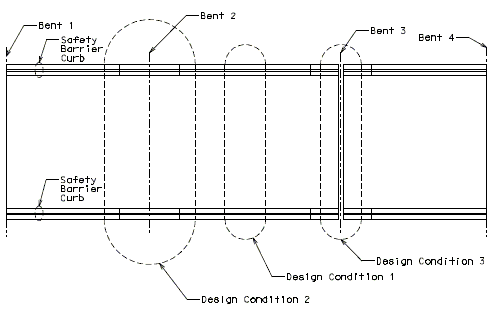
Design Conditions
Two design conditions can exist for the slab interior.
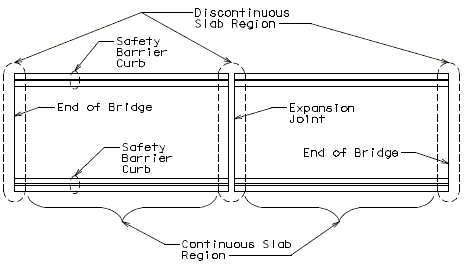
Design Condition 1 – Continuous Slab, where the slab section under consideration is not near an end bent or expansion joint.
Design Condition 2 – Discontinuous Slab, where the slab section under consideration is at an end bent or expansion joint.
Critical Sections
The critical design section for negative moments may be taken as follows:
| For steel girders - | the design negative moment should be taken at<br\>1/4 of the flange width from the centerline of the web. |
| For P/S-I girders - | the design negative moment should be taken at 1/3<br\>of the flange width, but not exceeding 15” from the<br\>centerline of the web |
The critical design slab section for positive moment shall be taken at location of maximum positive moment – generally midway between girders.
Width of Equivalent Strip at Continuous Slab Section
| For Positive Moment | |
| For Negative Moment |
Where:
| = equivalent strip width (in) | |
| = spacing of centerline to centerline of supporting components (ft) |
Width of Equivalent Strip at Discontinuous Slab Section
The effective strip width shall be taken as ½ of the equivalent strip width for a continuous slab section plus the distance between the transverse edge of slab and the edge beam (if any).

Determining Live Load
Slab interior live load design moments may be determined using Appendix Table A4-1 of the LRFD Specifications, provided that the assumptions used in the table are appropriate. It is assumed that the table is only applicable to continuous sections of slab (not at joints). It may be used at discontinuous sections by adjusting the tabulated moments as follows:
Where:
| = equivalent strip width (in). | |
| = vehicular dynamic load allowance. |
Note: includes multiple presence factor, .
Alternatively, the designer may use other sources to determine the design moments. For example any capable computer program for finite element design may be used.
The general methodology for applying live load to slab on girder with transverse primary strips is:
- Model the bridge cross section.
- Define the design vehicle (design truck).
- Move the design vehicle between the barrier curbs and add additional design vehicles as required to produce the maximum force effect. The wheel load shall not be closer than 1 ft. to the face of safety barrier curb and wheel loads of adjacent design vehicles shall not be closer than 4 ft. The design lane is assumed to occupy a 10 ft. width. Partial trucks (i.e. one wheel) should not be used.
Determining Dead Load
Although P/S Panel option is the standard for construction (when allowed), it may be assumed for slab analysis that slab is cast-in-place (CIP). The maximum negative and positive dead load moment may be taken to be:
Continuous over 4 girders (equally spaced):
Continuous over 5 girders (equally spaced):
Where:
| = moment at centerline of exterior girder due to: slab, future wearing surface, SBC, sidewalk, and other dead load components | |
| = center-to-center girder spacing |
Determining Top Reinforcing
The top (negative) reinforcing steel may be determined by assuming the section to be either singly- or doubly-reinforced, as needed.
Determining Bottom Reinforcing
The bottom (positive) reinforcing steel may be determined by assuming the section to be either singly- or doubly-reinforced, as needed. A 1” wearing surface shall be removed from the effective depth, .
Minimum Limit of Reinforcement
The amount of tension reinforcement shall be adequate to develop a factored flexural resistance, , a least equal to the lesser of either:
- 1.2 times the cracking strength determined on the basis of elastic stress distribution and the modulus of rupture, , of the concrete.
- 1.33 times the factored moment required by the applicable strength load combinations specified in LRFD Table 3.4.1-1
Shrinkage and Temperature Reinforcement
The area of reinforcing for top longitudinal steel, As, shall not be less than:
Where:
| = area of top longitudinal reinforcement | |
| = gross area of slab section (in^2) |
Maximum spacing of longitudinal reinforcement =
- 5 @ 15” are shown for standard slabs.
Distribution Reinforcement
The bottom longitudinal steel, as a percentage of the bottom primary reinforcement, shall not be less than:
Where:
| = effective span length (ft) specified in LRFD 9.7.2.3. It is the distance between flange tips, plus the flange overhang, taken as the distance from extreme flange tip to the face of the web. |

Concrete Cover
Existing (pre-LRFD) MoDOT concrete cover requirements for bridge slabs will be retained here. The cover requirements that follow meet or exceed LRFD requirements.
| At Bottom of CIP slabs | 1.00 in |
| Bottom of CIP slab over P/S P/C panels | 1.00 in |
| Top reinforcing | 3.00 in preferred |
| 2.75 in absolute min. |
Spacing Limits
LRFD 5.10.3.1.1 Minimum clear spacing between parallel bars in a layer:
| Maximum of: | 1) 1.5 where is bar diameter (in) |
| 2) 1.5 times maximum aggregate size (*) | |
| 3) 1.5 in |
(*) see Missouri Standard Specifications for Highway Construction
Bar Development
The calculated force effects in reinforcement shall be developed on each side of the critical section.
Cracking Check
Actual Stress
A transformed cracked section analysis shall be used with SERVICE-I moments to determine actual stress in reinforcing.
The spacing of mild steel reinforcement in the layer closest to the tension face shall satisfy the following:
in which:
Where:
| = exposure factor | |
| = .75 for class 2 exposure condition. | |
| = actual thickness of concrete cover measured from extreme tension fiber to center of the flexural reinforcement located closest thereto (in) | |
| = tensile stress in steel reinforcement at the service limit state (ksi) |
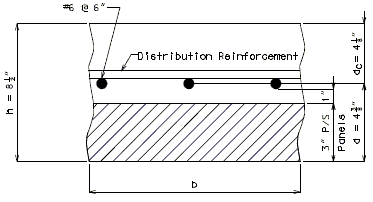
Reinforcing Placement
Although LRFD Specifications allow slab primary reinforcing to be skewed with the bridge under certain cases, MoDOT Bridge practice is to place transverse reinforcing perpendicular to roadway
Note: Due to the depth of cover and location of primary reinforcement, the cracking check shown on the previous page does not appear to be accurate for Missouri’s bridge decks shown above.
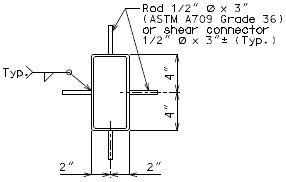
Negative Moment Steel over Intermediate Supports
Dimension negative moment steel over intermediate supports as shown.
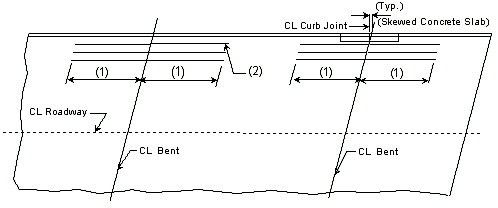
| (1) | Bar length by design | |
| (2) | Reinforcement placed between longitudinal temperature reinforcing in top. | |
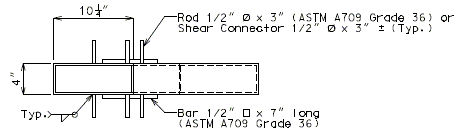
| Bar size: | #5 bars at 7 1/2" cts. (Min.) | |
| #8 bars at 5" cts. (Max.) | ||
Steel Structures:
| (1) | Extend into positive moment region beyond "Anchor" Stud shear connectors at least 40 x bar diameter x 1.5 (Epoxy Coated Factor) (*) as shown below. |
| (2) | Use #6 bars at 5" cts. between longitudinal temperature reinforcing in top. |
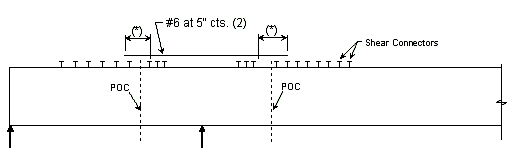
Locations of termination of reinforcement steel in the deck slab for Prestressed Structures shall be checked for the following criteria and adjusted as necessary:
- No more than 50 percent of the reinforcement shall be terminated at any section.
- Adjacent bars shall not be terminated in the same section.
- Flexural reinforcement shall be extended beyond the point at which it is no longer required to resist flexure for a distance not less than:
- The effective depth of the member
- 15 times the nominal diameter of bar
- 1/20 of the clear span (centerline to centerline of pier)
- Continuing reinforcement shall extend not less than the development length, ld, beyond the point where reinforcement is no longer required to resist flexure.
- At least one third of the total tension reinforcement provided for negative moment at a support shall have an embedment length beyond the point of inflection not less than:
- The effective depth of the member
- 12 times the nominal diameter of bar
- 0.0625 times the clear span (centerline to centerline of pier)
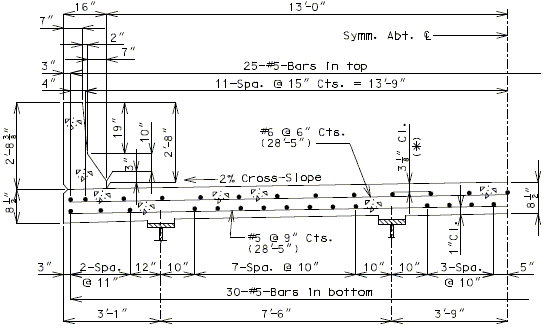
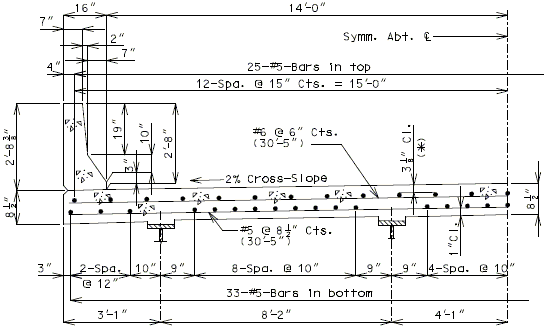
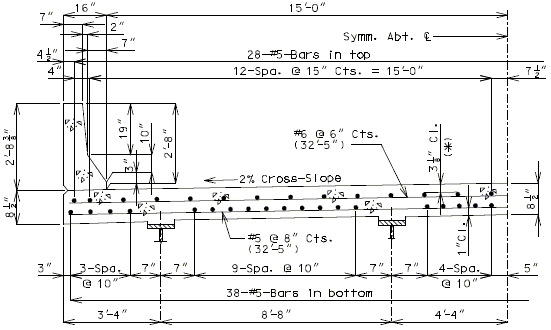
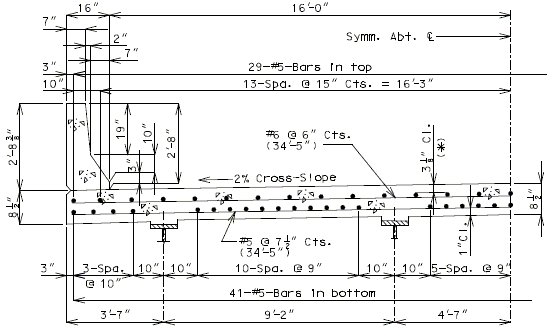
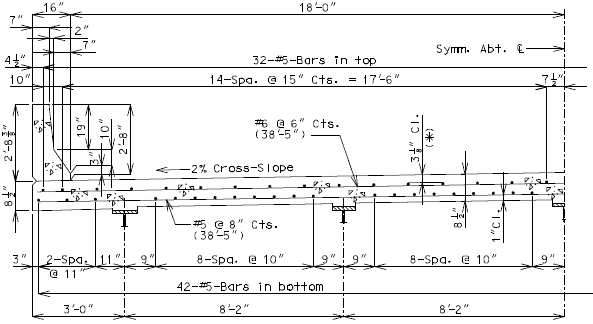
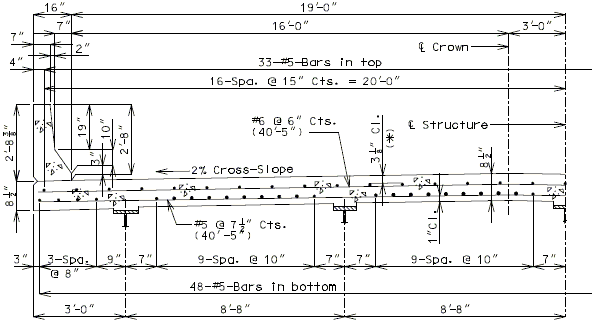
751.10.1.6 Slab Overhang Section Design
Girder Layout
In order to use distribution factors provided in LRFD Table 4.6.2.2.2 for girder design, the roadway overhang shall not exceed 5.5 ft.
Slab Thickness
The slab overhang shall be 8 1/2” slab thickness.
Design Cases
Four design cases shall be considered for each design condition.
| Design Case 1 | EXTREME EVENT II load combination with transverse and longitudinal collision force components |
| Design Case 2 | EXTREME EVENT II load combination with vertical collision force components (Does not control slab for TL-4). |
| Design Case 3 | STRENGTH I load combination |
| Design Case 4 | SERVICE I load combination for cracking check |
Design Conditions
Three design conditions may exist for slab overhang design.
| Design Condition 1 – | Continuous Slab & Continuous SB |
| Design Condition 2 – | Continuous Slab & Discontinuous SBC |
| Design Condition 3 – | Discontinuous Slab & Discontinuous SBC |
Critical Sections
The critical design section for slab overhang shall be at the following two locations:
- At roadway face of safety barrier curb
- At exterior girder:
- For steel girders – the design negative moment should be taken at ¼ of the flange width from the centerline of the web.
- For P/S-I girders - the design negative moment should be taken at 1/3 of the flange width, but not exceeding 15” from the centerline of the web.
|
|
| SBC Loading | Slab Design Loading |
| DESIGN CASE 1 | |
|---|---|
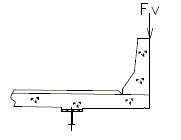
| |
| DESIGN CASE 2 | |
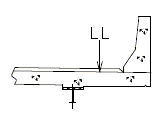
| |
| LL = vehicular live load | |
| DESIGN CASE 3 | |
Width of Equivalent Strip at Continuous Slab Section
The equivalent strip width for a continuous section of slab overhang shall be:
Where:
| = equivalent width (in) | |
| = distance from load to point of support (ft) |
Width of Equivalent Strip at Discontinuous Slab Section
LRFD 4.6.2.1.4c The effective strip width shall be taken as 1/2 of the equivalent strip width for a continuous slab section plus the distance between the transverse edge of slab and the edge beam (if any). This shall not be taken to be greater than equivalent strip width for continuous slab section.
Assumed Load Distribution
To determine the load effect at slab overhang critical sections, the slab shall be assumed as fixed at the exterior girder. This assumption is intended for slab design only, not the distribution of slab loads to girder.
For the purpose of determining the collision load effect at slab critical sections, the load may be assumed to fan out at 30 degrees on each side from the point of load.
Determining Top Reinforcing
The top (negative) reinforcing steel may be determined by assuming the section to be either singly- or doubly-reinforced, as needed. For slab overhang lengths equal to or less than 3’-10”, the reinforcement shown in the standard slab details is adequate (see EPG 751.10.1.7). For overhang lengths greater than 3’-10”, further analysis is required for top transverse steel design.
Effect of Slab Drains
The effect of slab drain openings in the slab overhang shall be considered. Their effect may be considered by ensuring the following:
Where:
| = area of steel provided over the strip width including effect of drain openings | |
| = area of steel required over strip width by calculation |
Reinforcing Criteria
Reinforcing limits, cover, temperature steel, distribution steel, and placement shall be the same as for Slab Interior Section.
Special Considerations for SBC-Mounted Light Pole
Standard details for mounting 30 ft. and 45 ft. Type B light poles on safety barrier bridge curb are provided. At the barrier curb-to-slab interface, the force effect of wind on the light pole (STRENGTH - III) with 90 m.p.h. wind is less than that due to EXTREME EVENT-II (TL-4) on safety barrier bridge curb. Therefore, reinforcing designed for EXTREME EVENT-II (TL-4) load combination will be adequate.
751.10.1.7 Standard Slab Details
| ( A ) | Although P/S panel slabs are the standard, C.I.P. cross section are shown for information. |
| ( B ) | This slab design includes an allowance for 35 psf future wearing surface. |
| ( C ) | Slab design is based on ultimate strength design, f’c = 4 ksi, and grade 60 reinforcing steel. |
| ( D ) | Haunching diagrams shall be provided for only the P/S panel slab. |
| ( E ) | Quantities for haunching are estimated by taking 4% of slab quantities for steel structures and 2% for prestressed structures. |
| ( F ) | When the flange width exceeds the bottom longitudinal reinforcement spacing over the girder, reduce the bar spacing between the girders and increase the bar spacing over the girder to clear the flange edges. |
| ( G ) | When the structure is on grade, determine lengths of the longitudinal reinforcement in the slab and safety barrier curb from the actual length. |
| ( H ) | For slab design, the centerline of wheels is located 1 foot from face of curbs. |
| ( I ) | The standard slabs were designed assuming 12” minimum flanges. |
| ( J ) | When median barrier curb or safety barrier curb is permanently required on the structure, other than at the edge of slab, P/S panels are not recommended in the bay underneath the curb. Check reinforcement in the C.I.P bay for collision and wheel loads on opposite faces of the curb and provide suitable anchorage of the reinforcing steel. |
| ( K ) | The bridge roadway width, from gutter line to gutter line, shall be the same as the roadbed width (from outside edge of shoulder to outside edge of shoulder). |
| ( L ) | The P/S panels are recommended to be used in at least two consecutive bays. |
| ( M ) | Standard slabs do not include the effect of features not shown (i.e. sidewalk, fence, utilities, etc…) except for future wearing surface. |
| ( O ) | Minimum concrete cover for slab top bars is 2 ¾” for #8 longitudinal bars. |
| Note: | Generally, when the deck is bid in Sq. Yd., curbs are bid in linear Ft., and when the deck is bid in Cu. Yd., curbs are bid in Cu. Yd. |
| * Cover will be less for greater than #5 longitudinal bars. |
751.10.1.8 Epoxy Coated Reinforcement
GENERAL
All reinforcement in the slab and above, and all reinforcement that extends into the slab, shall be epoxy coated; also, any wing reinforcement that extends into the safety barrier curb shall be epoxy coated.
NON-INTEGRAL END BENTS WITH EXPANSION DEVICES
The #6 bars in the end bent backwall above the upper construction joint shall be epoxy coated. V-bars in the backwall shall also be epoxy coated.

751.10.1.9 Standard Parabolic Crown
Use parabolic rounding for all bridges at the crown of the roadway except for the bridges with superelevated slabs. The profile grade will be at the intersection of the two cross-slopes if it is located at the crown of the roadway.
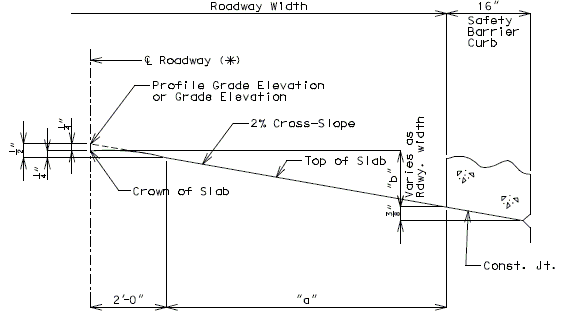
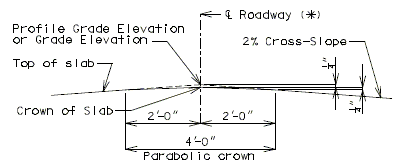
751.10.1.10 Profile Grade & Vertical Curve Data
PROFILE GRADE
See the Design Layout for location of the profile grade.
Generally, the profile grade is at the centerline of roadway for two-way traffic bridges.
For one-way traffic bridges (as used in standard divided highways), the profile grade is at some other location away from the centerline of roadway.
Generally, the profile grade will be shown in the cross section through the superstructure on the slab sheet and in the plan view on the front sheet of the design plans.
Show stations and profile grade elevations for all bents in the plan view on the front sheet of the design plans.

VERTICAL CURVE DATA
Place the vertical curve data on the front sheet near the elevation view at the vertical curve P.I. station, or as near to the vertical curve P.I. station as practical.

A crest vertical curve detail is shown. If the bridge is located on a sag vertical curve, then the detail for a sag vertical curve is to be used.
751.10.1.11 Slab Elevations
Slab elevations are used to determine haunching at the tenth points of steel and prestressed girder spans over seventy-five feet in length. Spans less than seventy-five feet in length use quarter points.
Theoretical Bottom of Slab Elevations at Centerline of Girder (Prior to Forming for Slab)
Elevations and details for Theoretical Bottom of Slab Elevations at Centerline of girder (prior to forming for slab) shall be provided on all stringer or girder type structures.
Steel Girders
Elevations are determined by adding DL1 and DL2 deflections to finished bottom of slab elevations. DL1 deflections are reduced by the percent of dead load deflection due to the weight of structural steel. DL2 deflections are reduced by the percent of dead load deflection due to future wearing surface.
P/S I-Girders
Initial camber minus final camber is used to determine DL1 deflection.

- (**) Elevations are based on a constant slab thickness of 8 1/2" and include allowance for theoretical
dead load deflections due to weight of Slab (including Prestressed Panel) and Barrier Curb.
- (**) Elevations are based on a constant slab thickness of 8 1/2" and include allowance for theoretical

| Example: | |
|---|---|
| 972.0715 | Finished top of Slab Elevation at centerline of girder |
| - 0.7083 | Slab Thickness |
| 971.3632 | Finished Bottom of Slab Elevation at centerline of girder |
| + 0.0478 | Theoretical Dead Load Deflection due to weight of slab and barrier curb. |
| 971.4110 | Theoretical Bottom of Slab Elevation at centerline Girder (Prior to Forming for Slab) |
| 971.41 | (USE) Theoretical Bottom of Slab Elevation at centerline Girder (Prior to Forming for Slab) |
and
Simple Span Plate Girder and Wide Flange Girder Design and Details

- (**) Elevations are based on a constant slab thickness of 8 1/2" and include allowance for theoretical
dead load deflections due to weight of Slab (including Prestressed Panel) and Barrier Curb.
- (**) Elevations are based on a constant slab thickness of 8 1/2" and include allowance for theoretical

| Example: | |
|---|---|
| 830.7504 | Finished top of Slab Elevation at centerline of girder |
| - 0.7083 | Slab Thickness |
| 830.0421 | Finished Bottom of Slab Elevation at centerline of girder |
| + 0.1348 | Theoretical Dead Load Deflection due to weight of slab and barrier curb. |
| 830.1769 | Theoretical Bottom of Slab Elevation at centerline Girder (Prior to Forming for Slab) |
| 830.18 | (USE) Theoretical Bottom of Slab Elevation at centerline Girder (Prior to Forming for Slab) |
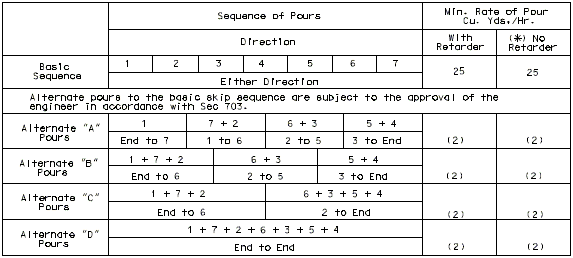
751.10.1.12 Slab Pouring Sequences
Concrete pouring and finishing with/without rates are based on the following:
One pouring sequence must be provided that will permit a minimum pouring rate of 25 cubic yards per hour without retarder for steel structures and with retarder for prestressed structures. A minimum finishing rate of 20 linear feet per hour is also required. If these two requirements conflict, see the Structural Project Manager.
Continuous steel structures will normally require a case I pouring sequence with the basic sequence being a skip pour arrangement. Minimum yardage for the basic sequence shall not be less than 25 cubic yards per hour. Computation of minimum yardage for alternate pours is outlined below. If the rate for the alternate pours should be 25 yards or less, the skip pour basic sequence may be eliminated with the first alternate pour becoming the basic sequence.
Use of retarder is required for prestressed structures and a case II sequence * is normally required. The minimum rate of pour will be determined by the 20 feet per hour minimum finishing rate but shall not be less than 25 cubic yards per hour. For span lengths over 80'or special structures (segmental, etc.), see Structural Project Manager.
- = Slab width (out to out of curbs, or width being poured)(ft.)
- = 8 1/2" (slab thickness)
- = Volume of concrete (cu. yds./hr.)
- (two span) = Length of longest alternate "A" pour (ft.)
- (more than two span) = Length of longest span (ft.)
(*) Case II sequence is used for all prestressed structures, except if slab area of one span is greater than 3,000 sq. ft., use case I.
Minimum rate of pour/hour for alternate pours (reduce V by 25% for P/C P/S Panels).
| Without Retarder: | |
|---|---|
| Not less than | |
| With Retarder: | |
| Not less than | |
| Simple Span: | |
| Not less than | |
Extra long span or extra wide bridges that indicate a basic rate greater than 25 cu. yds. per hr. are to be checked with the Structural Project Manager.
The minimum rate of pour for solid slab or voided slabs is 20 linear feet of bridge per hour and not less than 25 cu. yds. per hour. Check pouring rates with Structural Project Manager if it is indicated necessary to exceed the basic minimum rate of 25 cu. yds. per hour.
The largest minimum rate of pour for alternate pours is 50 cu. yds. per hour in rural areas or 65 cu. yds. per hour in urban areas.
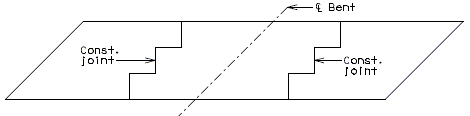
Slab Pouring Sequence Transverse Construction Joints
Slab Pouring Sequence - Bridges on Grade
All bridges on straight grades shall be poured up grade.
All bridges on vertical curves may be poured either up or down grade.
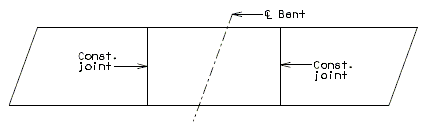
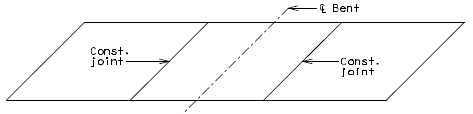
Transverse Construction Joint
On occasion, it will be necessary to off-set the transverse construction joint. For example, on bridges with large skews, wide roadways or short spans, the transverse construction joint could extend across the intermediate bent. Should this occur, the off-set or sawtooth construction joint shall be used.
It is desirable to relocate const. joint within reason (6"±) should it cross additional negative slab reinforcement. However, this shall not be considered critical.
Since the off-set construction joint creates construction problems, the designer shall avoid its use, if possible. Consult the Structural Project Manager for possible variations. See illustrations below for clarification.
Longitudinal Construction Joints
Wide Flange Beam, Plate Girder and Prestressed Girder
Normally, the maximum finishing width is 54'. Larger widths require longitudinal construction joints. Normally, the widest section of slab shall be poured first. During construction, the engineer may opt to eliminate this construction joint. Include note (H6.18) on roadways with longitudinal construction joints to address this option.
The finishing width shall be adjusted to finish the surface approximately parallel to the skew (i.e., skewed transverse construction joints) if the angle of skew exceeds or if the angle of skew exceeds and the ratio of placement width divided by span lengths equals or exceeds 0.8.

|
| Wide Flange Beam or Plate Girder |
|---|
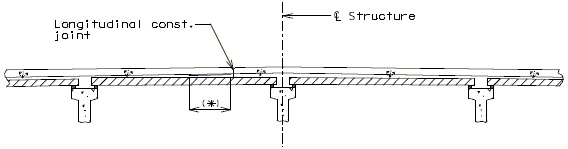
|
| Prestressed Girder |
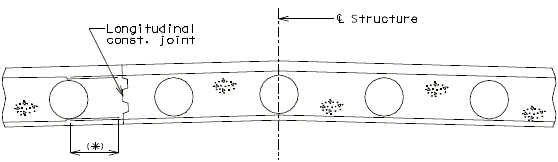
|
| Voided Slab |
| (*) See Lap Splices of Tension Reinforcement - 751.5 Standard Details |

|

|
| Typical Section thru C.I.P. Slab Construction Joint | Typical Section thru Precast Panel Slab Construction Joint |
|---|
Pouring and Finishing Concrete Roadway Slabs
| Span Ratio n | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Spans | Coef. | 1.0 | 1.1 | 1.2 | 1.25 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 2 | a | .4 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3 | a | .4 | .35 | .30 | .28 | .25 | .22 | .20 | .19 | .18 | .17 | .16 | .15 |
| 3 | b | .15 | .18 | .21 | .25 | .30 | .33 | .35 | .36 | .37 | .38 | .39 | .40 |
| 4 & 5 | a | .4 | .35 | .30 | .28 | .25 | .22 | .20 | .19 | .18 | .17 | .16 | .15 |
| 4 & 5 | b | .15 | .18 | .21 | .25 | .30 | .33 | .35 | .36 | .37 | .38 | .39 | .40 |
| 4 & 5 | c | .15 | .18 | .21 | .25 | .30 | .33 | .35 | .36 | .37 | .38 | .39 | .40 |
Use adjacent spans for ratio n.
Span lengths to be used are center to center of bearing.
Modify the dimensions produced by the coefficients on wide roadways and large skews if they produce construction joints that are within 6" of the additional negative slab reinforcement.
Dimensions, except for terminal lengths of end spans, shall be to the nearest foot.
For 6 & 7 spans, use same coefficients for a, b, & c as for 4 & 5 spans.
PLATE GIRDER AND PRESTRESSED CONCRETE: (2-SPAN)
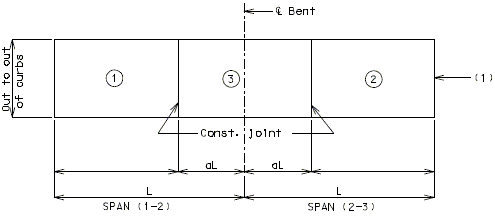

PLATE GIRDER AND PRESTRESSED CONCRETE: (3-SPAN)
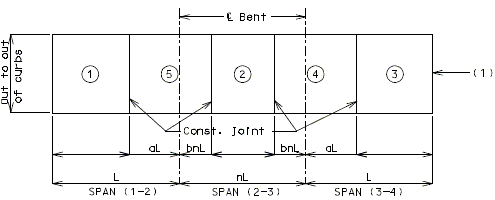

I-BEAM, PLATE GIRDER AND PRESTRESSED CONCRETE: (4-SPAN)
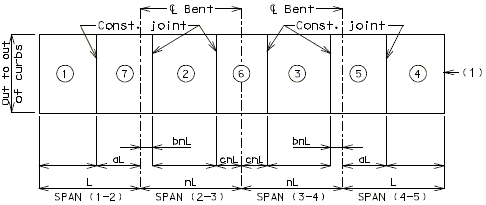
I-BEAM, PLATE GIRDER AND PRESTRESSED CONCRETE: (5-SPAN)


PRESTRESSED CONCRETE: (2-SPAN)
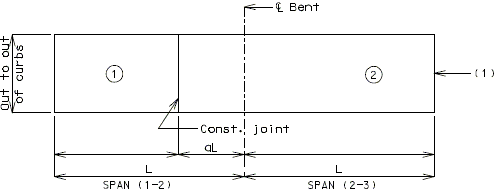

PRESTRESSED CONCRETE: (3-SPAN)
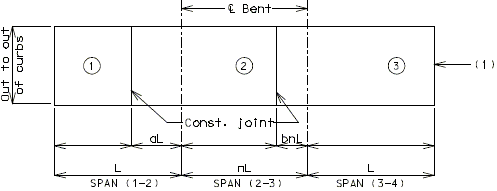

PRESTRESSED CONCRETE: (4-SPAN)
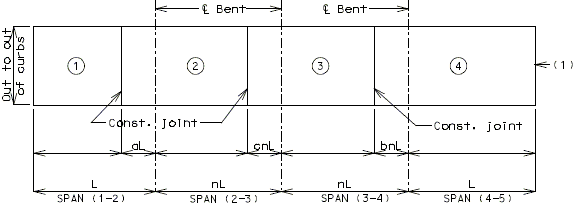

PRESTRESSED CONCRETE: (5-SPAN)
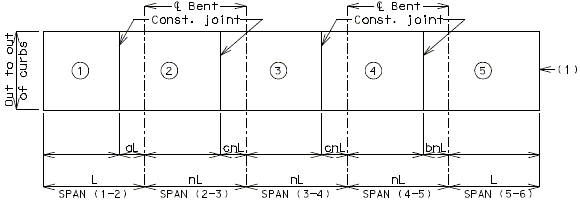

| Note: | Pouring sequence used on prestressed concrete with a basic rate of 25 cu. yds./hr. When multi-series of spans are used - see Structural. Project Manager. Slab pours shown are to be reversed for bridges on a minus grade. |
| (1) | Fill face of end bent or appropriate exposed plates, angles, wide flanges, and joint filler required for expansion devices. Note: For prestressed structures, "aL" and "bnL" may be made shorter than that indicated by the coefficients to balance pours. |
| (2) | Minimum pour rates. |
751.10.1.13 Drip Bevel
Single Drip Bevel

Use a single drip bevel on all standard bridges, the low side of superelevated bridges, the high side of superelevated continuous concrete slab bridges, and at medians.
Double Drip Bevel

Use a double drip bevel on the high side of all superelevated bridges (except continuous concrete slab bridges), and box girder bridges.
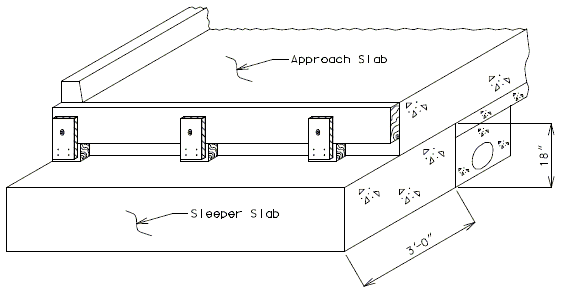
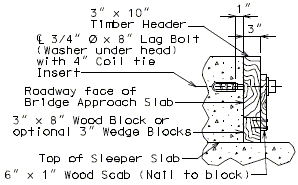
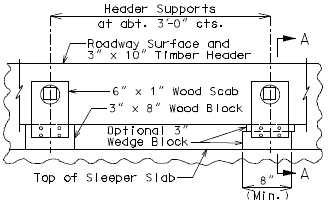
751.10.1.14 Timber Header
751.10.2 Stay in Place Deck Formwork
751.10.2.1 Prestressed Panels - Design
Design Criteria
Precast prestressed concrete panels shall be 3” thick with 5.5” cast-in-place concrete slab. Panel concrete strength shall be = 6.0 ksi and = 4.0 ksi. Cast-in-place slab shall be of strength = 4.0 ksi. The panels are considered as beams for analysis and design.
Prestressing steel shall be AASHTO M 203 (ASTM A 416) – Uncoated Seven-Wire, Low-Relaxation Strands. The strands will be grade 270 ksi, have a nominal diameter of 3/8”, area of 0.085 , and be spaced at 4.5” in the panels.
| = ultimate strength of strands = 270 ksi | |
| = yield strength of strands = 0.9 = 243 ksi | |
| = modulus of elasticity of strands = 28,500 ksi |
Panels shall be set on joint filler in accordance with Sec 1057.6 of Missouri Standard Specifications or polystyrene bedding material. Filler thickness shall be a minimum of 1” and a maximum of 2”. Standard filler width is 1.5” except at splice plates where 3/4” minimum is allowed to clear splice bolts. Joint filler thickness may be reduced to a minimum of 1/4” over splice plates on steel structures. The joint filler thickness may also be varied within these limits to offset girder camber or at the contractor’s option a uniform 1” (min.) thickness may be used throughout. The same thickness shall be used under any one edge of any panel and the maximum change in thickness between adjacent panel shall be 1/4”.
As per the above criteria, the following shall control the panel width, measured parallel to the prestressing strands:
- Maximum Panel Width = 9’-6”
- Minimum Panel Width = 4’-0”
Precast prestressed panels are recommended to be used in at least two consecutive bays.
When a median barrier curb is permanently required on the structure, precast prestressed panels are not recommened to be allowed in the bay underneath the curb.
Note: Units of stress are in ksi.
Load Definitions
Non-Composite Loading – This is the loading that occurs before the cast-in-place concrete slab hardens and acts compositely with the prestressed panels. The contributions to the Non-Composite Loading are as follows:
- Precast Prestressed Panel, DC
- Cast-In-Place Slab, DC
- Additional Slab Weight due to excess haunch, DC
- Construction Load of 50 lb/ft2
Composite Loading – This is the loading that occurs after the cast-in-place concrete slab hardens and acts compositely with the prestressed panels. The contributions to Composite Loading are as follows:
- Future Wearing Surface, DW
- Safety Barrier Curb, DC
- Design Live Load, LL
Prestress Losses
Refined estimates of time-dependent losses are used, based on LRFD 5.9.5.4, as opposed to approximate lump sum estimate of losses in LRFD 5.9.5.3.
The prestress losses shall be calculated to investigate concrete stresses at two different stages.
- Temporary stresses immediately after transfer:
- Final stresses
Load Combinations for Stress Checks
Construction Loading = DC + 0.050 ksf with Effective Prestressing Force
- Allowable Concrete Tensile Stress =
- Allowable Concrete Compressive Stress =
Service I = Permanent Loads with Effective Prestressing Force
- Allowable Concrete Compressive Stress =
Service I = Live Load + Half the Sum of Permanent Loads and Effective Prestressing Force
- Allowable Concrete Compressive Stress =
Service I = 1.0DC + 1.0DW + 1.0LL with Effective Prestressing Force
- Allowable Concrete Compressive Stress =
Service III = 1.0DC + 1.0DW + 0.8LL with Effective Prestressing Force
- Allowable Concrete Tensile Stress =
Strength I = 1.25*DC + 1.5*DW + 1.75LL with Effective Prestressing Force
- Factored Moment Resistance =
- Where:
- = as calculated in LRFD 5.5.4.2.1
Reinforcement Check
- Minimum Requirement =
751.10.2.2 Prestressed Panels - Details

|

| |
| Panels-Squared Ends | Panels-Skewed Ends | |
|---|---|---|
| PLAN OF PRECAST PRESTRESSED PANELS PLACEMENT | ||
751.10.2.3 Steel Corrugated Bridge Forms
(Generally Curved Steel Structures)
(Use only with approval of the Structural Project Manager)


751.10.3 Bridge Deck Drainage - Slab Drains
751.10.3.1 Type, Alignment, Spacing
Type
Slab drains shall be 8" x 4" x 1/4" steel tubing whenever possible.
Alignment
All standard crown roadways shall have the 8" x 4" steel tubing placed with the 8" side perpendicular to the curb whenever possible. All super-elevated roadways shall have the 8" x 4" steel tubing placed with the 8" side parallel to the curb.
Slab Drain Spacing
Slab drain spacing shall be designed according to the 1986 FHWA report "Bridge Deck Drainage Guidelines" along with information acquired from the 1995 University of Missouri Rolla report "Scupper Interception Efficiency." The following general guidelines may be refined if justified by appropriate calculations by other methods of design such as FHWA “HEC 21, Design of Bridge Deck Drainage”. The variations to the design and general requirements listed below should be discussed with the appropriate Liaison or Project Manager on a project by project basis before incorporated into the final design.
General Requirements for Location and Spacing of Slab Drains
- Drains shall be spaced no closer than 8 ft. center to center.
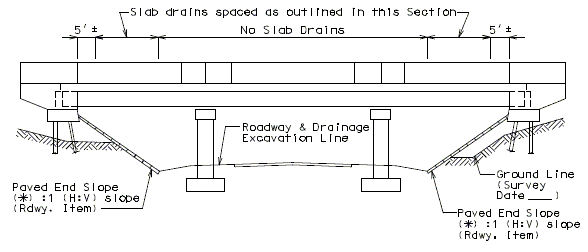
- Drains shall be omitted on high side of super-elevation bridges.
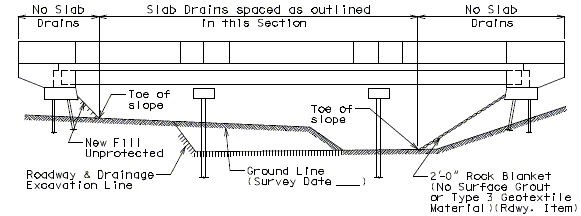
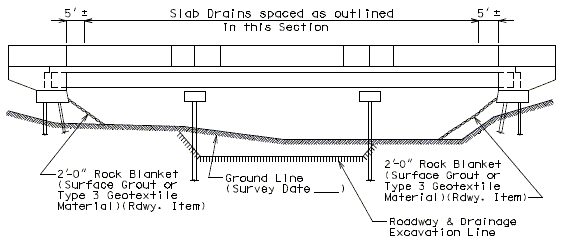
- Drains shall not be located over unprotected fill. If drains are needed, fill should be protected with use of; rock blanket with surface grout, rock blanket with type 3 qeotextile, or concrete slope protection.
- Drains shall be omitted on all grade separations and rail overpasses except when located over concrete slope protection or as noted on Design Layout.
- For Bridges with slopes less than 0.5%, space drains at about 10 ft. centers where possible.
- Use consistent spacing for drains when possible.
- Drains shall be placed at least 5 feet from the face of substructure beam.
- Drains shall be dimensioned along centerline of exterior girder to facilitate placement of coil inserts or holes in girders.
- For all sag vertical curves, locate the points at which the slope is 0.5% on either side of the low point, and space drains on 10 ft. centers between them where possible. Use equations in this section for spacing drains for the remainder of the curve.
- If location restrictions apply, the same number of drains as calculated by equations in this section shall be placed on the bridge when possible. The designer is responsible for relocating drains.
- The length of the approach slab shall be included in the length of the bridge for spacing computations. Do not place slab drains on the approach slab.
Calculation of spacing to first slab drain
The first slab drain either side from the high point of the bridge shall be calculated according the following equation. If the value of L1 is greater than the bridge length, slab drains are not required.
- = Distance from high point to first slab drain (ft.)
- = Cross slope of slab (ft./ft.)
- = Longitudinal slope of bridge (ft./ft.). For vertical curve bridges, "S" is the longitudinal slope at the location of the drain being analyzed. A linear approximation can be used to simplify the calculations.
- = Design spread (ft.). The spread is the width of gutter flow. The spread for any bridge with a 3 ft. or more shoulder width should be taken as 6 ft. If the shoulder width is less than 3 ft., the spread shall be the shoulder width plus 3 ft.
- = Ratio of impervious to pervious drain area. On a bridge deck, most rainfall runs off, except at the beginning of a storm when rain wets the bridge deck and fills small depression areas. Design of slab drain spacing assumes the bridge deck is wetted, therefore a "" value of 1.0 is recommended.
- = Manning's coefficient of friction. For typical pavements, "" equal to 0.016 is used.
- = Design rainfall intensity (in./hr.). The "Rational Method" as outlined in "Hydraulic Engineering Circular-12, (HEC-12)" with a 25 year frequency for a 5 minute time period shall be used to calculate the design rainfall. Missouri's intensity varies from 8.00 in./hr. to 8.50 in./hr. for this frequency and time period. Therefore an "" value of 8.50 in./hr. is recommended to determine slab drain spacing.
- = Width of deck drainage area (ft.). For crowned roadways use distance from top of crown to curb face and for super-elevated bridges use distance from face of curb to face of curb.
Calculation of Additional Slab Drain Spacing
Once the first slab drain has been located, slab drain efficiency "Es" is required to determine the location of additional slab drains. Given the efficiency of the slab drain, the amount of flow intercepted by the first slab drain (q)i is determined by (q)i =Es(QT)i where (QT) is the flow at which the gutter is filled to the design spread (T) at slab drain #1 and is determined by the equation:
- (cu. ft./second)
Interception flow decreases the flow in the gutter by q (intercepted). This flow must be replaced before another slab drain is required. Flow in the gutter at the second slab drain is given by the equation:
- (cu. ft./second)
Another slab drain is located when runoff minus intercepted flow equals flow in the gutter filled to the design spread at length where is the total length of bridge to .
For tangent sections the additional theoretical slab drain spacing are constant. For vertical curve sections the theoretical slab drain spacing are variable and require the designer to repeat the process till the end of the bridge. Theoretical spacing should be revised to consider ease of spacing.
Calculation of Slab Drain Interception Efficiency
Slab drain interception efficiency is that fraction of gutter flow removed by the slab drain. FHWA's report called "Bridge Deck Drainage Guidelines" gives an approximation for for small grates and low gutter velocities, which is a fraction of triangular gutter flow passing over a slab drain located next to the curb.
- = width of slab drain normal to the flow (ft).
- = Design spread.
In UMR's report "Scupper Interception Efficiency" imperical data is used to determine a more precise efficiency coefficient. They state that the slab drain efficiency can be closely approximated by the equation , where is a percent (%) and must be divided by 100 for use in the flow equations.
- = Longitudinal slope of bridge at slab drain location.
- and = Imperical coefficients dependent on the bridge cross-slope. The following tables can be used to determine and .
The UMR method shall be used whenever possible because of its ability to account for increased velocities with increased slopes in its efficiency coefficient. When the design spread "" is other than 6 feet, the FHWA method must be used.
| Cross-Slope | a | b |
|---|---|---|
| 0.010 | 14.580 | -0.180 |
| 0.016 | 6.670 | -0.340 |
| 0.020 | 3.550 | -0.450 |
| 0.030 | 2.080 | -0.500 |
| 0.040 | 2.080 | -0.440 |
| 0.050 | 3.680 | -0.280 |
| 0.060 | 5.510 | -0.140 |
| 0.070 | 4.550 | -0.160 |
| 0.080 | 5.420 | -0.110 |
| Cross-Slope | a | b |
|---|---|---|
| 0.010 | 9.170 | -0.230 |
| 0.016 | 7.060 | -0.280 |
| 0.020 | 5.620 | -0.320 |
| 0.030 | 4.670 | -0.320 |
| 0.040 | 3.060 | -0.370 |
| 0.050 | 3.660 | -0.300 |
| 0.060 | 4.560 | -0.210 |
| 0.070 | 5.500 | -0.130 |
| 0.080 | 5.420 | -0.110 |
751.10.3.2 Details
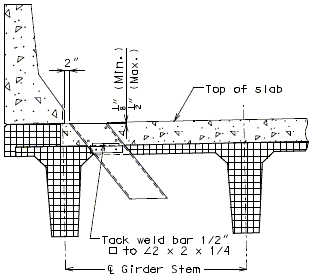
|
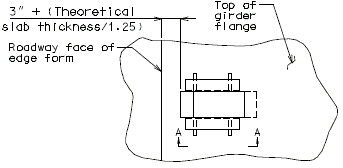
|
| Part Section of Slab at Drain | Part Plan of Drain Blockout |
|---|---|
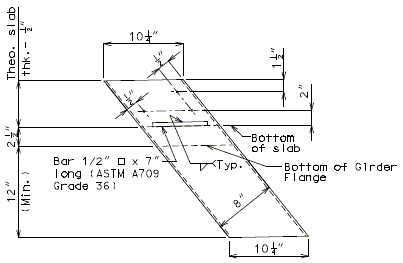
|

|
| Part Section A-A | |
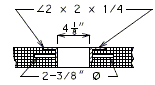
| |
| Elevation of Drain | Section B-B |
| |
| Plan of Drain | |

|

|
| Elevation of Drain | |
|---|---|
| |
| Part Section of Slab Drain | Plan of Drain |

| |
| Part Section Showing Bracket Assembly | |

|

|
| Elevation of Drain | |
|---|---|

| |
| Part Section of Slab Drain | Plan of Drain |

| |
| Part Section Showing Bracket Assembly | |
751.10.3.3 General Requirements for Location of Slab Drains
751.10.4 Conduit Systems
General
Conduit systems shall be provided on structures when specified on the Design Layout.
All Conduit shall be rigid non-metallic schedule 40 heavy wall PVC (Polyvinyl Chloride Plastic). Provide appropriate notes on plans.
All Conduit Clamps, if required, shall be commercially available conduit clamps approved by the engineer.
Size
Conduit size shall be specified on the Design Layout.
Location
Single 2" round conduit shall be placed in the slab.
Single conduit greater than 2" round shall be placed in the barrier curb (4" round max. for bridge without cantilever sidewalk, 3" round max. for bridge with cantilever sidewalk).
Placement of multiple conduit shall be determined on a case by case basis. Options include placing conduit on hangers, encasing conduit in concrete that is attached to slab, and encasing conduit in safety barrier curb if there is enough room. Multiple conduits are not allowed in curb when sidewalk is used.
See example details below.
Expansion Fittings
Expansion fittings shall be specified on the plans when conduit passes across expansion devices and filled joints, including filled joints in the barrier curb when conduit is located in the curb.
Expansion movements shall be specified at each location of an expansion fitting. Expansion fittings shall be able to accommodate movement one and a half times the designed expansion movement or 4 times the joint filler thickness rounded to nearest half inch.
- Example 1 - Plate Girder with expansion length of 300 ft.
- Use 2 1/2 inches.
- Example 2 - 1/4 " Joint filler in curb
- Use 1/2 inch.
Junction Boxes
Size and location of junction boxes shall be specified on the plans when a conduit system is used. The minimum size junction box for 2" round conduit is 12" x 12" x 4". The minimum size junction box for greater than 2" round conduit is 12" x 14" x 6". The minimum size junction box for 4" round conduit is 16" x 12" x 6". No more than one 4" round conduit shall be allowed in safety barrier curb and none are allowed when cantilever sidewalk is used due to clearance problems with reinforcement and inadequate concrete cover. Multiple conduits are not allowed in safety barrier curb when cantilever sidewalk is used. A junction box shall be located in a wing at each end of the bridge. Junction boxes shall also be located on the bridge when junction box spacing is greater than 250 feet. Junction boxes located in the slab or barrier curb shall preferably be located in areas accessible from underneath the bridge. See details of locations of junction boxes below.

| ||
| Part Elevation of Junction Box in Wing | ||
|---|---|---|

|

|

|
| Part Section A-A | Section of Junction Box in Slab |
Section on Junction Box in Barrier Curb |





![{\displaystyle \,W_{c}{\sqrt[{1.5}]{f'_{c}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c60eff5136bac036b16b0e4dd2d38cd372fe635f)














































































![{\displaystyle \,\phi M_{n}\geq Min.{\big [}1.2M_{cr},1.33M_{u}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eada8d2f5ea54da06c991b86ecb1d9e741d7e91)




























![{\displaystyle \,E_{S}=1-{\big [}1-(w/T){\big ]}^{2.67}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f514a8395683cd6077e87194e33c485e400b37)